Regression 9) Binary Dependent Vairable

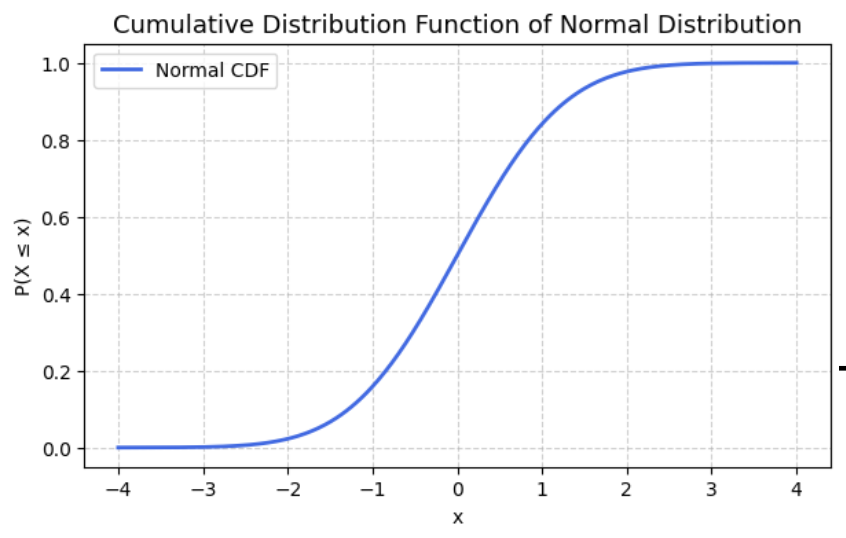
• cdf (Cumulative Distribution Funcion, 누적 분포 함수)

  ‘정규 분포의’ 특정 값 이하의 누적 확률

  확률값은 대칭적인 관계 : 표준정규분포 N(0, 1)에 대해 \(\Phi(-x) = 1 - \Phi(x)\)

MLE (Maximum Likelihood Estimation, 최대우도법)

파라미터 θ=(θ1,⋯,θm) 로 구성된 확률밀도함수 P(x

θ) 에서 관측 표본 데이터 집합을 x=(x1,x2,⋯,xn) 일 때, 표본으로부터 파라미터를 추정하는 방법

• x=(x1,x2,⋯,xn) : 표본 데이터 => 이미 관측된 고정값
• θ=(θ1,⋯,θm) : 모수(분포) => 아직 모르는 변수

=> “데이터(x)가 주여졌을 때, 각 모수(분포, θ)가 얼마나 가능성 있는가”

Likelihood

관측 데이터가 특정 분포로부터 나왔을 가능도

1. 표본 데이터 집합 관측

X = \{1, 4, 5, 6, 9\} 

1. 이 데이터가 추출되었을 것으로 생각되는 후보 분포(θi) 추출

   

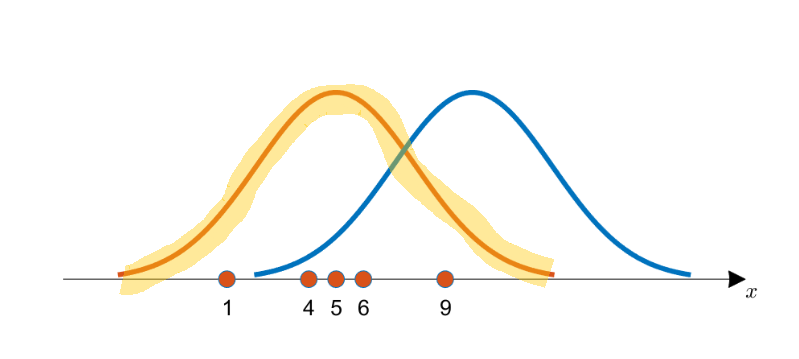
2. Likelihood Value(가능도) 구하기

   

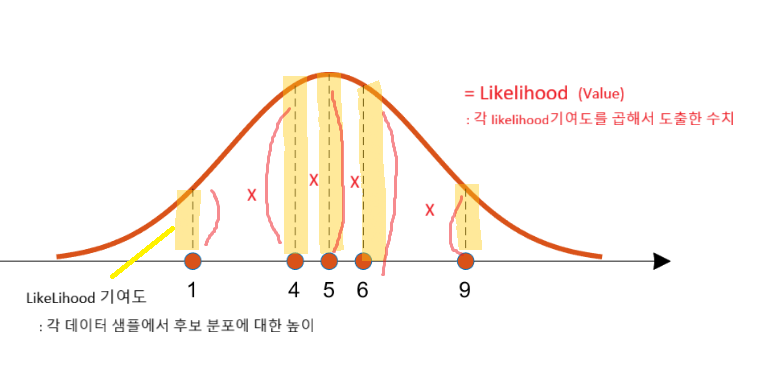
P(X|θi)=n∏k P(Xk|θi)

​

1. Likelihood Function (가능도 함수) 로 변환

   ‘θ’를 변수로 둠 <-> 관측 데이터(X)가 주여졌을 때, 모수 θ가 그럴듯할 정도(P(x

   θ))를 나타내는 θ에 대한 함수

   보통 자연로그를 이용해 log-likelihood function을 사용한다.

   L(θ|x)=logP(x|θ)=n∑i logP(xi|θ)
   

2. Maximum Likelihood Estimator 도출

   가능도 함수를 최대로 만드는 θ 찾기

   \hat{\theta }_{MLE}=arg\:\underset{θ}{max} L(θ)
   

#####